tim philip williams :: Generating castles for Minecraft™ using Haskell

Introduction

My kids and I have enjoyed building various structures in the game Minecraft, but it can get rather monotonous placing blocks one-at-a-time. I took a very brief look at the custom “mods” available, but wanted something more compositional, hence the idea for a Haskell DSL was born. The aim is to build a skeleton structure, thereby eliminating the most repetitive parts of manual construction, for example walls, floors, roofs etc. We can then enjoy furnishing the structures by hand in the actual game.

I haven’t yet distilled down the optimal set of primitives and combinators for all buildings/structures, but what I have so far seems usable and sufficient for generating castles such as these:

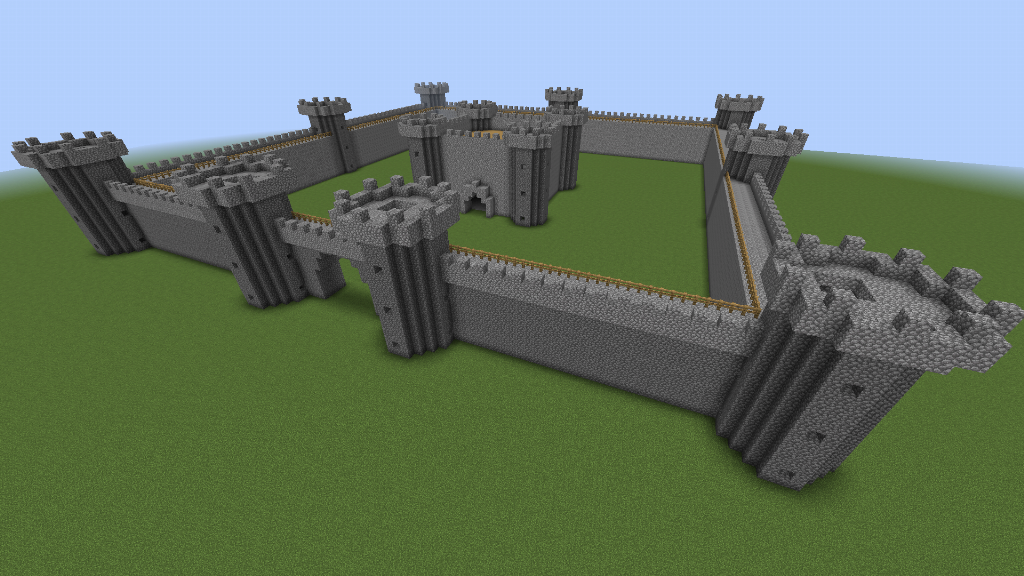
I use some continuous floating-point maths for computing circles and spirals, but it seems to work fine even when rasterized down to a small number of Minecraft blocks.

Finally, note that I have only ever tested this on the original Java version of Minecraft.

Preliminaries

Before we model the above in Haskell, let’s enable some extensions and import some modules:

{-# LANGUAGE GeneralizedNewtypeDeriving #-}
{-# LANGUAGE RankNTypes #-}
{-# LANGUAGE RecordWildCards #-}
{-# LANGUAGE ScopedTypeVariables #-}
{-# LANGUAGE TemplateHaskell #-}
{-# LANGUAGE ViewPatterns #-}

module Minecraft where

import           Prelude hiding (repeat, replicate, floor)
import           Control.Arrow
import           Control.Lens (Lens', view, over, set, makeLenses)
import           Control.Monad
import           System.FilePath
import           System.IO
import           System.Random
import           Text.Printf
import qualified Data.Map as Map

We will also use lenses to represent the three dimensions. This will allow us to write code that can read and update an abstracted dimension using only one function parameter, rather than passing getters and setters around. The only lens library functions we will use are as follows:

view :: Lens' a b -> a -> b
over :: Lens' a b -> (b -> b) -> a -> a
set  :: Lens' a b ->       b  -> a -> a

Data types

The basic atom in Minecraft is the block. Each block has coordinates, a kind (e.g. air, cobblestone, water) and some optional state (which we won’t make use of here).

type Kind  = String
type State = String

data Block = Block
    { _blockCoord :: Coord
    , _blockKind  :: Kind
    , _blockState :: Maybe State
    }
    deriving Show

data Coord = Coord { _x :: Int, _y :: Int, _z :: Int }
    deriving (Ord, Eq)

instance Show Coord where
    show (Coord x y z) = show (x, y, z)

makeLenses ''Coord
makeLenses ''Block

Minecraft structures are represented as an ordered list of blocks, wrapped in a newtype, in order to hide the underlying representation. We will be working with lists of Blocks soon and so the newtype helps us distinguish between the layers.

newtype Blocks = Blocks { unBlocks :: [Block] }
    deriving (Semigroup, Monoid, Show)

mkBlocks :: [Coord] -> Blocks
mkBlocks = Blocks . map (\c -> Block c cobblestone Nothing)

-- | A block of nothing (air) at the origin (0,0,0)
zero :: Blocks
zero = Blocks [Block (Coord 0 0 0) air Nothing]

mapBlocks :: (Block -> Block) -> Blocks -> Blocks
mapBlocks f = Blocks . map f . unBlocks

mapKind :: (Kind -> Kind) -> Blocks -> Blocks
mapKind f = mapBlocks $ over blockKind f

We set the kind of block using an infix # operator:

-- | Set the kind of all blocks
infixr 8 #
(#) :: Blocks -> Kind -> Blocks
(#) blocks k = mapKind (const k) blocks

We derive semigroup and monoid using the underlying list instances. The semantics of the Blocks monoid is that of a non-commutative monoid, the right-hand-side overrides the left. For example:

zero <> (zero # cobblestone) -- results in a cobblestone block at (0,0,0)
(zero # cobblestone) <> zero -- results in nothing (an air block) at (0,0,0)

Abstracting over dimensions using lenses

We will abstract over dimensions using lenses:

type Dimension = Lens' Coord Int

We have the lenses x, y and z automatically generated for us using Template Haskell. Note that Minecraft uses the convention where x and z are in the horizontal plane and y is the height. This convention continues to confuse me and was the cause of most of the bugs in my structure generation. I follow it here, only to be consistent with Minecraft.

The use of lenses means that we can use a single dimension parameter for functions that read coordinates, update them or both.

-- | Move blocks by 'i' in dimension 'd'.
move :: Dimension -> Int -> Blocks -> Blocks
move d i = mapBlocks $ over (blockCoord . d) (+i)

-- | Translate blocks by the supplied 'x, y, z' offset.
translate :: Int -> Int -> Int -> Blocks -> Blocks
translate x' y' z' = move x x' . move y y' . move z z'

-- | Get the coordinate bounds for blocks along a particular dimension 'd'.
bounds :: Dimension -> Blocks -> (Int, Int)
bounds d blocks = (minimum ps, maximum ps)
  where
    ps = map (view $ blockCoord . d) $ unBlocks blocks

This centering function is particularly useful and is simplified by using a single dimension lens parameter:

-- | Centre blocks on the origin of the supplied dimension.
centre :: Dimension -> Blocks -> Blocks
centre d blocks = move d (- (w `div` 2) - mn) blocks
  where
    w        = mx - mn
    (mn, mx) = bounds d blocks

centre_xz :: Blocks -> Blocks
centre_xz = centre x . centre z

Building our first structure

To build structures we will need combinators that provide us with repetition. The simplest one that sprang to my mind was the following:

-- | Repeat structure 'n' times with function 'f' applied iteratively.
repeat :: (Blocks -> Blocks) -> Int -> Blocks -> Blocks
repeat f n = mconcat . take n . iterate f

I then used repeat to define a combinator that will replicate a structure using a particular spacing (probably because I had castle crenellations in mind!).

-- | replicate structure 'n' times with a spacing 's' in dimension 'd'.
replicate :: Dimension -> Int -> Int -> Blocks -> Blocks
replicate d s = repeat (move d s)

A common use for replicate would be to define a simple line of blocks, which we will default to cobblestone:

-- | Create a line of cobblestone blocks with length 'n' along dimension 'd'.
line :: Dimension -> Int -> Blocks
line d n = replicate d 1 n zero # cobblestone

Similarly we can define walls, floors and squares of cobblestone:

wall :: Dimension -> Int -> Int -> Blocks
wall d w h = replicate y 1 h $ line d w

floor :: Int -> Int -> Blocks
floor lx lz
    = replicate x 1 lx
    . replicate z 1 lz
    $ zero # cobblestone

square :: Int -> Blocks
square w =
    l x <> move z (w-1) (l x) <>
    l z <> move x (w-1) (l z)
  where
    l :: Dimension -> Blocks
    l d = line d w

squareWall :: Int -> Int -> Blocks
squareWall w h = replicate y 1 h (square w)

-- | A square roof of thickness 't' and width 'w'.
squareRoof :: Int -> Int -> Blocks
squareRoof t w = mconcat
    [ translate i 0 i $ square (w-2*i)
    | i <- [0..t-1]
    ]

A square of crenellations is similar to a square, but we place the blocks with a spacing of two. It works best with odd widths, e.g. 5, 7, 9 etc.

squareCrenellations :: Int -> Blocks
squareCrenellations w =
    l x <> move z (w-1) (l x) <>
    l z <> move x (w-1) (l z)
  where
    l :: Dimension -> Blocks
    l d = replicate d 2 (w `div` 2 + w `rem` 2) blk
    blk = zero # cobblestone

We now have enough to define a square turret complete with windows and crenellations!

squareTurret :: Int -> Int -> Blocks
squareTurret w h = mconcat
    [ squareWall w h
    , translate (-1) h (-1) $ mconcat
        [ floor w' w'
        , squareWall w' 2
        , move y 2 (squareCrenellations w')
        ]
    , translate (w `div` 2) 1    0  windows
    , translate (w `div` 2) 1 (w-1) windows
    ]
  where
    w'      = w + 2
    windows = replicate y 3 (h `div` 3) zero

To get this structure into Minecraft, we need to generate an “.mcfunction” text file of commands that can be executed by the game. The only command we will use is “setblock” which takes three coordinates and a block kind. But before Minecraft will load such a file, we need to create a “datapack” inside a particular level. The level I used was called “Castles” and for my Linux machine, Minecraft saved game state was stored in ~/.minecraft. I created the following directories:

[tim@x1c:~/.minecraft/saves/Castle/datapacks]$ find
.
./haskell
./haskell/data
./haskell/data/haskell
./haskell/data/haskell/functions
./haskell/pack.mcmeta

The content of pack.mcmeta was as follows:

{
 "pack": {
 "pack_format": 3,
 "description": "Tim's data pack"
 }
}

Before we generate the mcfunction file, we first prune the block list to get rid of any overridden blocks (alternatively we could write a new monoid instance to do this as it goes along).

-- | Removes unnecessary setblock instructions from the list.
prune :: Blocks -> Blocks
prune = Blocks . Map.elems . Map.fromList . map (_blockCoord &&& id) . unBlocks

Finally here is the “render” function for generating the commands:

data CoordKind = Relative | Absolute

render :: FilePath -> String -> String -> CoordKind -> Blocks -> IO ()
render minecraftDir levelName functionName coordKind (prune -> blocks) =
    withFile filePath WriteMode $ \hnd ->
        forM_ (unBlocks blocks) $ \(Block Coord{..} kind mstate) ->
          hPutStrLn hnd $ printf
              (case coordKind of { Relative -> "setblock ~%s ~%s ~%s %s %s"
                                 ; Absolute -> "setblock %s %s %s %s %s" })
              (show _x) (show _y) (show _z) kind (maybe "" (\s -> "["++s++"]") mstate)
  where
    filePath = foldr (</>) (functionName ++ ".mcfunction")
                   [ minecraftDir, "saves", levelName, "datapacks"
                   , "haskell", "data", "haskell",  "functions" ]

Minecraft has a default limit of 65K blocks in an mcfunction file and it’s easy to go past this limit when generating large complex structures, fortunately it is possible to increase this limit using the command “/gamerule maxCommandChainLength”.

To render our square turret to an “mcfunction” file, use the following at the Haskell prompt:

λ> let t = square_turret 9 15
λ> render "~/.minecraft" "Castles" "square_turret" Relative t

To render in absolute coordinates, you will need to translate (and possibly centre) the structure first. Note that F3 can be used in the game to find your current coordinates. The advantage of using absolute coordinates, is that it allows us to re-generate the structure over the top of the previous one to fix any minor issues. We can also remove structures from the game, by re-rendering using # air to set all blocks to empty (air).

Now it’s time to load Minecraft. Enter the level you have the datapack installed into and press t to bring up the prompt. To create the turret at your current position, enter the following (tab completion should work):

/reload
/function haskell:square_turret

If Minecraft cannot see the mcfunction file, check that it can see the [file/haskell] datapack by entering /datapack list. If all is well, you should see something like this:

Circles, Spirals and Cones

A square turret obviously works well in Minecraft, but I wondered how effective it would be to attempt to rasterize a circular turret. I tried the simplest implementation I could think of:

-- | A circle of radius r in the plane formed by dimensions (d, d'), centered on (r,r).
circle :: Dimension -> Dimension -> Int -> Int -> Blocks
circle d d' r steps = move d r . move d' r $
    mkBlocks [ set d x . set d' z $ Coord 0 0 0
             | s <- [1..steps]
             , let phi = 2*pi*fromIntegral s / fromIntegral steps :: Double
                   z   = round $ fromIntegral r * cos phi
                   x   = round $ fromIntegral r * sin phi
             ]

circleWall :: Int -> Int -> Int -> Blocks
circleWall r h steps =
    replicate y 1 h (circle x z r steps)

Note that the number of steps can be varied, with low values being useful for circular placement of windows and crenellations. A solid circle is even easier:

-- | A filled circle of radius r in the plane formed by dimensions (d, d'), centered on (r,r).
solidCircle :: Dimension -> Dimension -> Int -> Blocks
solidCircle d d' r = move d r . move d' r $
    mkBlocks [ set d x . set d' z $ Coord 0 0 0
             | x <- [-r..r]
             , z <- [-r..r]
             , let r' = sqrt (fromIntegral $ x*x + z*z) :: Double
             , r' <= fromIntegral r
             ]

-- | A solid cylinder of radius r in the plane formed by dimensions (d, d') and with length along dl.
solidCylinder :: Dimension -> Dimension -> Dimension -> Int -> Int -> Blocks
solidCylinder d d' dl r h = replicate dl 1 h $ solidCircle d d' r

It would be nice to also create a staircase inside the circular turret, which we can generate using a spiral:

-- | An upward spiral in the (x,z) plane centered on (r,r).
spiral :: Int -> Int -> Int -> Int -> Blocks
spiral r h revs steps = translate r 0 r $
    mkBlocks [ Coord x y z
             | s   <- [1..steps]
             , let phi = 2*pi*fromIntegral (revs*s) / fromIntegral steps :: Double
                   z   = round $ fromIntegral r * cos phi
                   x   = round $ fromIntegral r * sin phi
                   y   = round $ fromIntegral (h*s) / (fromIntegral steps :: Double)
             ]

spiralStairs :: Int -> Int -> Int -> Int -> Int -> Blocks
spiralStairs r t h revs steps = mconcat
    [ translate i 0 i $ spiral (r-i) h revs steps
    | i <- [0..t-1]
    ]

My circular turret with a spiral staircase, crenellations, windows and a top floor with exit hole was thus:

circularTurret :: Int -> Int -> Int -> Blocks
circularTurret r h steps = mconcat
    [ solidCylinder x z y r h    # air -- clear space
    , translate 1 0 1 $ spiralStairs (r-1) 3 h 3 (3*steps) -- spiral staircase
    , circleWall r h steps
    , translate (-1) h (-1) (solidCircle x z r' <> -- upper floor
                             circleWall r' 2 (2 * steps) <> -- upper wall
                             move y 2 (circle x z r' (steps `div` 2))) -- crenellations
    , translate 2 h 2 $ floor 3 3 # air -- exit for staircase
    , move y 1 $ replicate y (h `div` 3) 3 (circle x z r 4) # air -- windows
    ]
  where r' = r + 1

In Minecraft, the circular turret has rasterized reasonably well and the spiral staircase inside works well:

My kids prefer the Germanic style of castle, most often seen in Disney movies, so I had a go at adding a conic top to the circular turret:

-- | An upright hollow cone in the (x,z) place centered on (r,r).
cone :: Int -> Int -> Int -> Blocks
cone r h steps = mconcat
    [ translate (r - r') y (r - r') $ circle x z r' steps
    | y <- [0..h]
    , let r' = round $ fromIntegral (r*(h-y)) / (fromIntegral h :: Double)
    ]

circularTurret_germanic :: Int -> Int -> Int -> Blocks
circularTurret_germanic r h steps =
    circularTurret r h steps <>
    translate (-1) h (-1)
         (move y 1 (circle x z r' 4) # air <> -- top windows
          move y 2 (cone r' 8 (2 * steps) # bricks)) -- cone roof
  where r' = r + 1

Grid Layouts

There are a whole host of layout combinators that we could imagine being useful, however for castles, a grid layout combinator should probably suffice. My implementation is:

grid :: Int -> [[Blocks]] -> Blocks
grid spacing = f z . map (f x . map centre_xz)
  where
    f :: Dimension -> [Blocks] -> Blocks
    f d = foldr (\a b -> a <> move d spacing b) mempty

Note that each grid item is centered horizontally on the origin before it is moved into position.

The Castle Keep

The castle keep is a large fortified building in the centre of the grounds. We’ll build ours from four turrets, four walls, three floors and an archway entrance.

castleKeep :: Blocks -> Int -> Int -> Blocks
castleKeep t w h = mconcat
    [ floors
    , squareWall w h
    , move y h (squareCrenellations w)
    , grid (w-1) [ [ t,  t]
                 , [ t,  t]
                 ]
    -- make a large archway that juts out
    , translate (w `div` 2) 0 (w-1) $ centre x $ archway 3 3
    ]
  where
    floors
        = translate 1 (-1) 1
        . replicate y 6 3
        $ floor w' w' # oak_planks
    w' = w - 2

An archway can be created from a larger solid arch (default stone) and overlaying a smaller empty space (air) arch.

--  | Make an archway of radius 'r' and thickness 't'.
archway :: Int -> Int -> Blocks
archway r t
    =  solidArch r t
    <> move x 1 (solidArch (r-1) t # air)

To create the solid arch, we overlay a solid circle and wall in the (‘x’,‘y’) plane and replicate it across ‘z’ to achieve thickness.

--  | Make a solid arch of radius 'r' and thickness 't'.
solidArch :: Int -> Int -> Blocks
solidArch r t
    = replicate z 1 t
    $ solidCircle x y r <> wall x (2*r + 1) r

Notice that the castleKeep definition is parameterised by a turret structure.

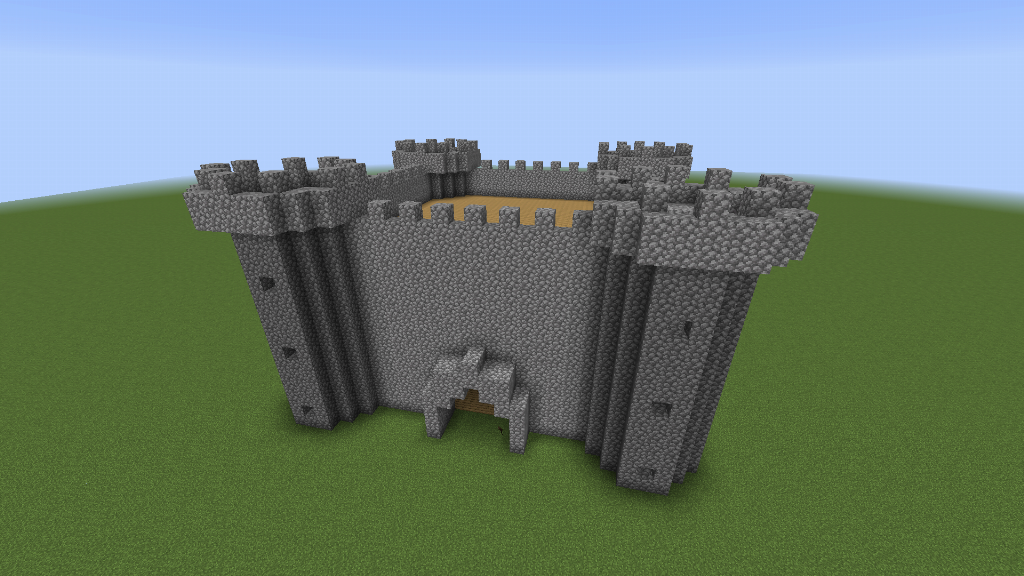
A Full Castle

The most important component of a English castle is the outer castle wall, so I made the one below quite elaborate. The wall has an archway entrance, an inner and outer skin, an overhang, crenellations and a wall-top fence. Feel free to add arrow slit windows and perhaps inner platforms, ladders and doors!

castleWall :: Int -> Int -> Blocks
castleWall w h = mconcat
    [ squareWall w h                             -- outer wall
    , translate 3    0  3 (squareWall (w-6) h)   -- inner wall
    , translate 1 (h-1) 1 (squareRoof 2 (w-2))   -- roof
    , translate (-1) (h-1) (-1)
        (squareWall (w+2) 2 <> move y 2 (squareCrenellations (w+2))) -- overhangs
    , translate 3 h 3 (square (w-6) # oak_fence)  -- wall top fencing
    , translate (w `div` 2) 0 (w-4) $ centre x $ archway 4 4
    ]

To create the final full castle, we start with the castle wall and then surround the keep by outer turrets and a gatehouse (two turrets close together at the entrance).

englishCastle :: Blocks
englishCastle = mconcat
   [ castleWall 100{-width-} 10{-height-}
   , grid 50 {-spacing-}
       [ [ t,  t,  t]
       , [ t,  k,  t]
       , [ t,  g,  t]
       ]
   ]
 where
   t  = circularTurret 4{-radius-} 15{-height-} 20
   k  = castleKeep (circularTurret 3{-radius-} 15{-height-} 20) 24{-width-} 15{-height-}
   g  = move x (-12) t <> move x 12 t -- gatehouse entrance has two turrets together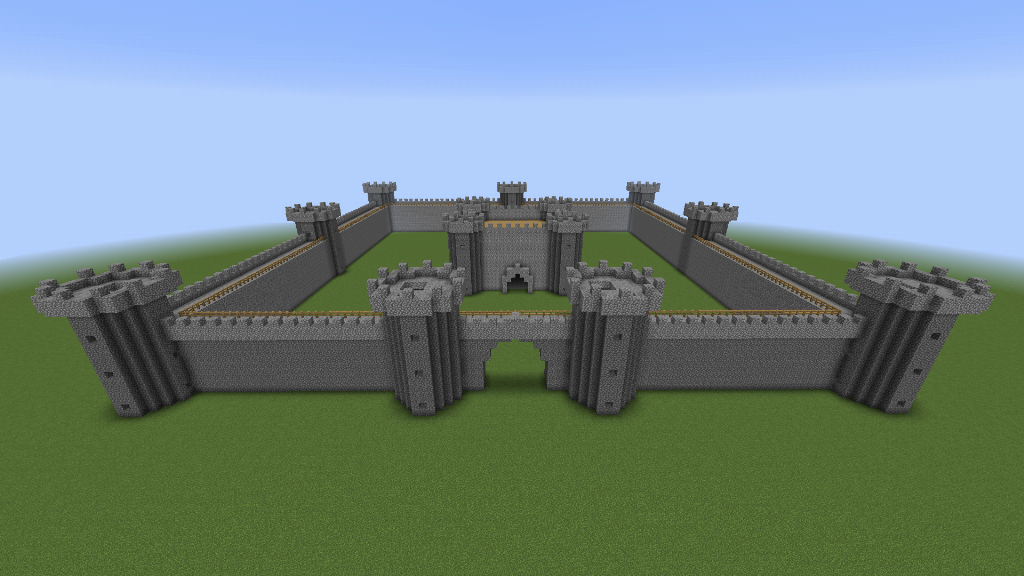

A Mossy Castle

Once we have generated a structure, we can modify it, perhaps by applying a random process. One idea is to make the castle mossy (see below), but one could also imagine many other effects such as creating a castle ruin!

randomise :: Double -> (Kind, Kind) -> Blocks -> IO Blocks
randomise p (from, to) (Blocks bs) =
    Blocks <$> mapM f bs
  where
    f b | view blockKind b == from = do
              r <- randomIO
              return $ if r < p
                       then set blockKind to b
                       else b
        | otherwise = return b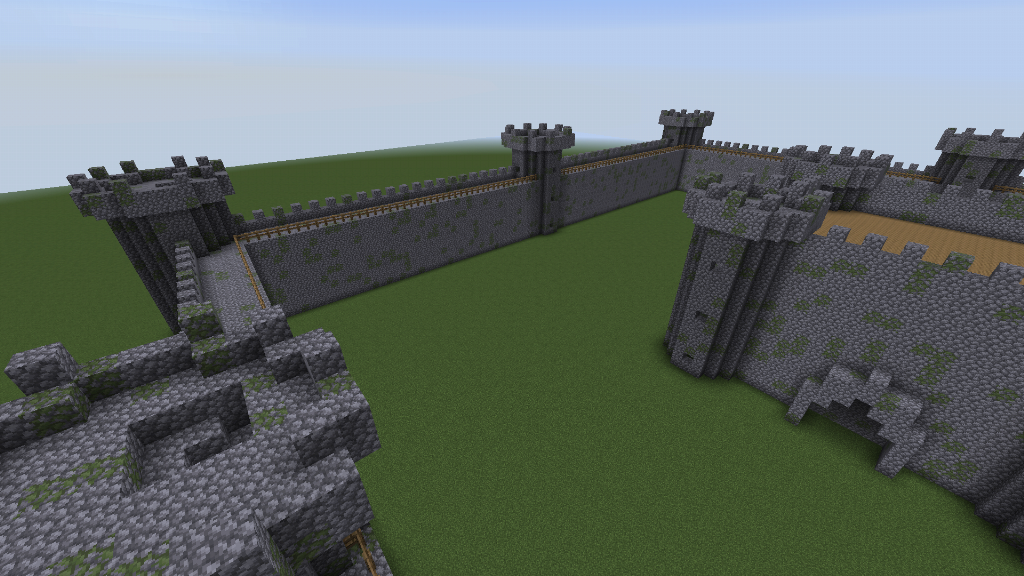

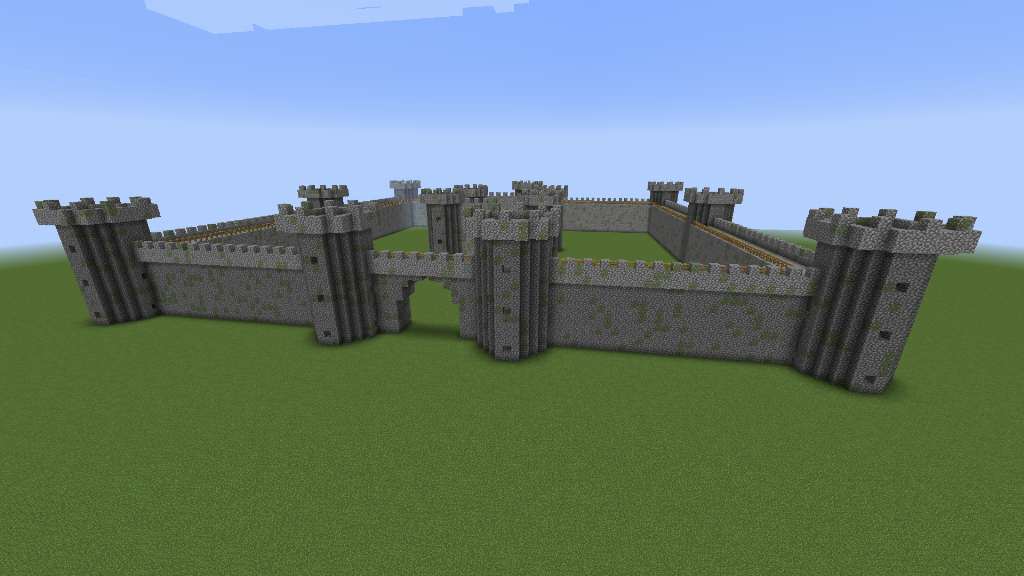
mossy :: Blocks -> IO Blocks
mossy = randomise 0.2 (cobblestone, mossy_cobblestone)

More Castles

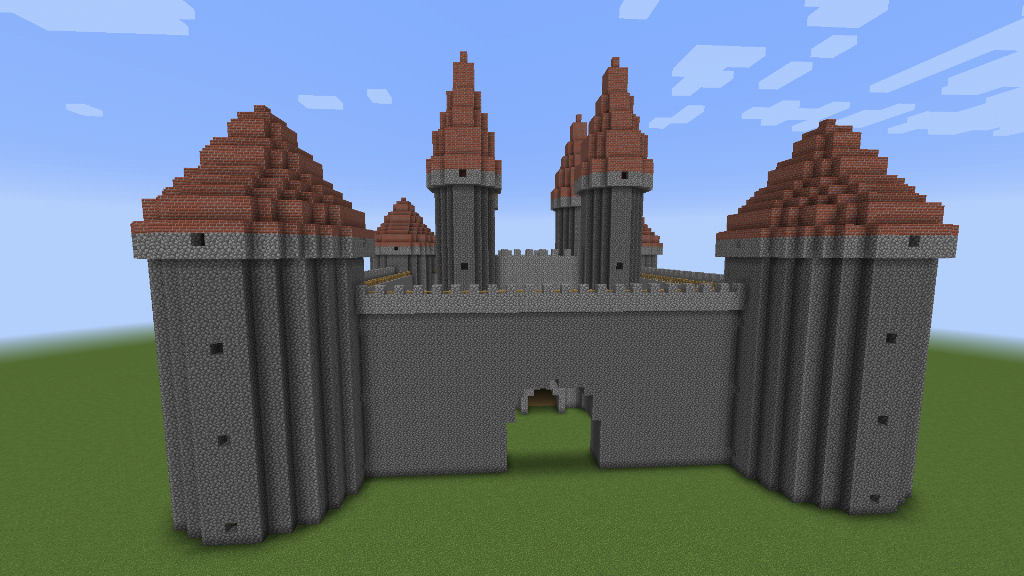
We can easily generate lots of variations on the castle theme, by changing the function parameters. For example, a Germanic castle, using our earlier Germanic turret:

A desert castle would be made of sandstone rather then cobblestone, thus we need a way to substitute a particular block kind for another:

-- | Substitute one block for another, intended to be used infix, e.g.
-- @ castle `subst` (cobblestone, sandstone) @
subst :: Blocks -> (Kind, Kind) -> Blocks
subst blocks (from, to) = mapKind f blocks
  where
    f k | k == from = to
        | otherwise = k

Have fun!

Note: the literal Haskell for this entire post can be found here.

Appendix

A selection of Minecraft block kinds

air = "air"
anvil = "anvil"
bed = "red_bed"
bookshelf = "bookshelf"
bricks = "bricks"
chair = "oak_stairs"
cobblestone = "cobblestone"
crafting_table = "crafting_table"
door_mat = "red_carpet"
enchanting_table = "enchanting_table"
furnace = "furnace"
glass_pane = "glass_pane"
ladder = "ladder"
mossy_cobblestone = "mossy_cobblestone"
oak_door = "oak_door"
oak_fence = "oak_fence"
oak_planks = "oak_planks"
sandstone = "sandstone"
spruce_stairs = "spruce_stairs"
spruce_wood = "spruce_wood"
table = "oak_planks"
torch = "torch"