The Essence of Compilation

Recently I was extolling the virtues of Haskell to a colleague–an important part of my day job–and the subject was compilers. I was essentially asserting that compilers and external DSLs (domain-specific languages) are a killer application for Haskell. To demonstrate this, I put together a simple tutorial compiler and virtual-machine, which I think catches the essence of compilation. We have only addition and constants in the input expression language (Hutton’s Razor [1]) and assume an inifinite supply of virtual-machine registers (as does the SSA-form used by LLVM [2]). We therefore do not need to concern ourselves with the details of register allocation.

To start with, we’ll need a bunch of imports. Note that two non-platform hackage packages are required: uu-parsinglib and wl-pprint.

import Control.Applicative
import Control.Monad.State
import Control.Monad.Writer (WriterT, execWriterT, tell)
import Data.Map (Map)
import qualified Data.Map as M
import Text.ParserCombinators.UU (pChainl)
import Text.ParserCombinators.UU.Utils
import Text.PrettyPrint.Leijen ((<+>), (<>), hsep, vsep, int
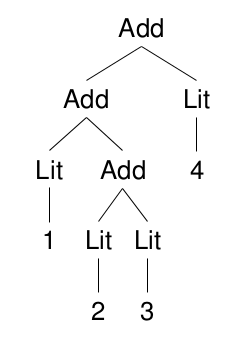
                               , text, punctuate, comma)

The abstract syntax tree (AST) is a simple inductive type–the ‘Add’ constructor takes two values of type ‘Exp’. The leaf nodes are literal integers (constants).

-- | abstract syntax tree
data Exp = Add Exp Exp
         | Lit Int
         deriving (Show)

We can define the denotational semantics of our language using the following structurally recursive function:

-- | denotational semantics
eval :: Exp -> Int
eval (Add x y) = eval x + eval y
eval (Lit i)   = i

The parser for our language makes use of the uu-parsinglib parser-combinator library, which allows us to compose smaller parsers into a larger parsers using combinators (functions that take parsers and return parsers). The resulting code often mirrors the formal grammar.

-- | the parser
parse :: String -> Exp
parse = runParser "Expression" pExp
  where
    pExp  = foldr pChainl pAtom [Add <$ pSymbol "+"]
    pAtom = Lit <$> pNatural
        <|> pParens pExp

λ> parse "1 + (2 + 3) + 4"
Add (Add (Lit 1) (Add (Lit 2) (Lit 3))) (Lit 4)
λ> eval it
10

Now that we have a parser and an AST, we can turn our attention to the code-generation phase. First we need to define some types for the instruction set we are targetting.

A program is an ordered list of instructions (statements):

type Program = [Inst]

An instruction is generally an opcode mnemonic followed by one or more operands (arguments). We only need one instruction to implement addition. Note that the first operand is the destination register.

data Inst = IAdd Reg Opd Opd
            deriving (Show)

Operands can either be immediate values or registers:

data Opd = Val Int -- ^ immediate value
         | Reg Reg -- ^ register
         deriving (Show)

Register names can simply be unique integers:

type Reg = Int

For our code generation phase, we will define a computation that maintains the next available register as state and writes out instructions as a side-effect. This computation will have the following type:

type Gen = WriterT [Inst] (State Reg)

The code generation function ‘gen’ is a structurally-recursive function on the AST. When given an expression, it returns a computation that when run, emits an ordered list of instructions as a side-effect and yields an operand result. The operand result only makes sense in the context of the previously emitted statements; and will ultimately represent the value of the expression during execution time.

gen :: Exp -> Gen Opd
gen (Add x y) = do
  o1 <- gen x
  o2 <- gen y
  r  <- new
  tell [IAdd r o1 o2]
  return $ Reg r
gen (Lit i) = return $ Val i

This part of the computation delivers fresh register names by modifying state:

new :: Gen Reg
new = modify succ >> get

Once we have recursed the AST and built our code-generation computation, we will need to run it to get the program (as a side-effect).

runGen :: Gen a -> Program
runGen = flip evalState 0 . execWriterT

Finally, we compose the phases together, to get a compiler:

compile :: String -> Program
compile = runGen . gen . parse

A pretty-printer helps visualise the output (see appendix). I’ve used the % prefix to indicate a register.

λ> putStrLn $ ppProg $ compile "1 + (2 + 3) + 4"
IAdd %1, 2, 3
IAdd %2, 1, %1
IAdd %3, %2, 4

To better understand the operational semantics, let’s define the virtual-machine that executes our instruction set. The virtual-machine is a stateful computation; we can represent its state as a map of register names to integer values.

type VM = State (Map Reg Int)

exec :: Inst -> VM ()
exec (IAdd r o1 o2) = do
  v1 <- load o1
  v2 <- load o2
  store r $ v1 + v2

load :: Opd -> VM Int
load (Val i) = return i
load (Reg r) = gets $ M.findWithDefault 0 r

store :: Reg -> Int -> VM ()
store r v = modify (M.insert r v)

run :: Program -> Map Reg Int
run = flip execState M.empty . mapM_ exec

Now we can visualise all the register contents:

λ> run $ compile "1 + (2 + 3) + 4"
fromList [(1,5),(2,6),(3,10)]

Note: the literal haskell for this entire post can be found here.

References

[1] G. Hutton, “Fold and unfold for program semantics,” ACM SIGPLAN Notices, vol. 34, no. 1, pp. 280–288, Jan. 1999.
[2] LLVM Language Reference

Appendix

A program pretty-printer.

ppProg :: Program -> String
ppProg = show . vsep . map ppInst
  where
    ppInst (IAdd r o1 o2) = text "IAdd" <+> ppOpds [Reg r, o1, o2]
    ppOpds                = hsep . punctuate comma . map ppOpd
    ppOpd (Val i)         = int i
    ppOpd (Reg r)         = text "%" <> int r