This post was originally titled “Generic recursion schemes for GADTs using fixed points of higher-order functors” – but that doesn’t really explain why one would go to all the trouble of writing code this way. The answer, of course, is that we obtain various proofs of correctness embedded within our static types. For example, we have a proof that our traversals are correct and that our syntax AST is well-typed, both before and after the transformations. As to whether the effort is worth it, I will leave that as an exercise to the reader!
One of my personal favourite applications of category theory applied to typed functional programming, is datatype generic programming using the fixed points of functors formed by parametrising the recursion. At my place of work, this technique has been used to great effect to write a rich set of standardised recursion schemes that work over many custom data types. In this post, I will attempt to explain how we have applied this technique to language syntax trees defined using Generalised Algebraic Data Types (GADTs). The jury is still out on whether the additional type-safety provided by GADTs is worth the added inconvenience of working with them in Haskell. I will let the reader decide for themselves rather than offer an opinion! Certainly Haskell and its libraries continue to improve in this area all the time.
Unfortunately we are going to need a fair few extensions to work effectively with GADTs:
{-# LANGUAGE GADTs #-}
{-# LANGUAGE KindSignatures #-}
{-# LANGUAGE RankNTypes #-}
{-# LANGUAGE TypeOperators #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE UndecidableInstances #-}
{-# LANGUAGE ViewPatterns #-}
{-# LANGUAGE DeriveFunctor #-}import Control.Arrow ((&&&),first)
import Data.Function (on)
import Data.Maybe (isJust, fromJust)
import Data.Monoid
import Text.PrettyPrint.Leijen hiding ((<>))Jumping straight in, for a simple expression abstract syntax datatype, with addition, multiplication and constants, the pattern functor representation would be:
with
An evaluation algebra for the above would thus be:
eval = cata alg where
alg :: ExprF Int -> Int
alg (Const i) = i
alg (Add a b) = a + b
alg (Mul a b) = a * bwhere “cata” is the catamorphism defined as:
The definition of cata can literally be read of the diagram below, with the four nodes representing types (objects) and the edges representing functions (morphisms).1
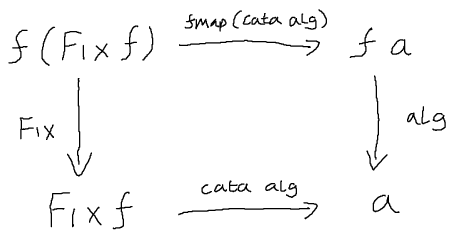
The point of such datatype generic programming is to define the recursion scheme (i.e. the fold function) once for all pattern functors; only the algebras need be specific to the datatype. We could implement, for example, a catamorphism for every datatype we define, but this approach would quickly get out-of-hand when working with many additional, sometimes complex, recursion schemes and large datatype definitions.
Let’s now introduce booleans into our expression syntax to support equality comparisons and conditionals. To do this using vanilla algebraic data types, we would need to create a new sum datatype which tags our result values as either integer or boolean:
Not only does this have a runtime cost during evaluation, more importantly it does not prevent incorrectly typed expression trees from being represented.
A GADT representation
If we wanted to utilise the newer GADTs to give us an efficient tagless representation and a type-safe invariant (only type-safe expressions are representable); we would start by writing down something like this:
data Expr :: * -> * where
Const :: Int -> Expr Int
Add :: Expr Int -> Expr Int -> Expr Int
Mul :: Expr Int -> Expr Int -> Expr Int
Cond :: Expr Bool -> Expr a -> Expr a -> Expr a
IsEq :: Expr Int -> Expr Int -> Expr BoolNote that we cannot even create the usual Functor, Foldable or Traversable instances for the above, since the a in Expr a is a type-index, which is refined during case analysis, not a vanilla type parameter that we are familiar with from parameteric polymorphism.
Let’s proceed to factor out the recursion as we did with the algebraic datatype example. Replacing all the points of recursion with a type parameter gives us this:
data ExprF :: (* -> *) -> * -> * where
Const :: Int -> ExprF r Int
Add :: r Int -> r Int -> ExprF r Int
Mul :: r Int -> r Int -> ExprF r Int
Cond :: r Bool -> r a -> r a -> ExprF r a
IsEq :: r Int -> r Int -> ExprF r BoolThe problem is that ExprF is no longer of kind * -> *, so we can’t use the recursion schemes defined for functors, such as cata above. When we tie the recursive knot, ExprF must become the type constructor Expr which is parametrised by the type (index) of the expression it represents. The type ExprF is therefore parametrised by a type constructor and the expression type. So how do we fix this? It turns out that we need a higher-order version of Fix, “HFix”. Note the pattern in the kind signatures below, we obtain the kind signature required for HFix by substituting (* -> *) for * in Fix. Redundant brackets have been added for clarity.
The type declaration of HFix is straightforward and follows from Fix:
We can now write:
Higher-order functors
Before we can define a recursion scheme for ExprF, we need to be able to map transformations over it. Our original datatype used for fixing with kind * -> *, had a functor instance. Just as we needed a higher-order version of Fix, we also need a higher-order, more general, functor definition. Such a higher-order functor, or HFunctor, would allow the mapping of Functors to Functors inside it. The type signature for this “hfmap” operation could be written as:
The functors f ang g (i.e. the recursive structures) being transformed, are parametrised by the type index a. Note that we require rank 2 universal quantifiers, because the function argument for hfmap must be polymorphic in the index type, in other words we need to universally quantify over type constructors f and g. Such a function is called a natural transformation in category theory and it is common to define the following type operator for it:
Using this notation, we shall move on to define a class for hfmap, HFunctor.
If you squint a bit, the above should look very familiar. The HFunctor instance for ExprF is very simple and is as follows:
instance HFunctor ExprF where
hfmap f (Const i) = Const i
hfmap f (Add x y) = Add (f x) (f y)
hfmap f (Mul x y) = Mul (f x) (f y)
hfmap f (Cond x y z) = Cond (f x) (f y) (f z)
hfmap f (IsEq x y) = IsEq (f x) (f y)For the higher-order recursion schemes, we can mechanically derive them from the vanilla Functor versions. For example, here is cata (again) and hcata.
Note that recent versions of GHC have some support for kind polymorphism via the PolyKinds extension, so we should be able to unify these two definitions in some way.
The hcata above, folds to a functor f and not to a value. So to write an evaluation algebra we will need an identity functor:
evalAlg :: ExprF I :~> I
evalAlg (Const i) = I i
evalAlg (Add x y) = (+) <$> x <*> y
evalAlg (Mul x y) = (-) <$> x <*> y
evalAlg (Cond x y z) = (\c t f -> if c then t else f) <$> x <*> y <*> z
evalAlg (IsEq x y) = (==) <$> x <*> yNote that I have assumed Functor and Applicative instances for I and lifted the application of operators, such as e.g. (+) into I. Personally I would rather use idiom brackets2, but they are not available in GHC Haskell.
Let’s test it with some example expressions:
λ> eval x
True
λ> eval y
1The interspersed HFix is also a mild inconvenience, but this could be hidden by defining new (smart) constructors, or perhaps an isomorphism with an unfixed representation.
If we want our fold to produce a final value of a constant type, independent of the expression type index, we will need the constant functor K. For example, we’ll need K in order to define a pretty-printer:
ppr :: Expr a -> Doc
ppr = unK . hcata alg where
alg :: ExprF (K Doc) :~> K Doc
alg (Const i) = K . text $ show i
alg (Add x y) = (\x y -> parens $ x <+> text "+" <+> y) <$> x <*> y
alg (Mul x y) = (\x y -> parens $ x <+> text "*" <+> y) <$> x <*> y
alg (Cond x y z) = (\x y z -> text "if" <+> x <+> text "then" <+> y <+> text "else" <+> z)
<$> x <*> y <*> z
alg (IsEq x y) = (\x y -> x <+> text "==" <+> y) <$> x <*> yλ> ppr x
(1 + 2) == 3
λ> ppr y
if (1 + 2) == 3 then 1 else 2For the common case of folding to a monoid, we can instead implement a higher-order analogue of the Foldable type class, starting with an “hfoldMap” method:
-- | Higher-order analogue of Foldable
class HFoldable (h :: (* -> *) -> * -> *) where
hfoldMap :: Monoid m => (forall b. f b -> m) -> h f a -> minstance HFoldable ExprF where
hfoldMap _ (Const _) = mempty
hfoldMap f (Add x y) = f x <> f y
hfoldMap f (Mul x y) = f x <> f y
hfoldMap f (Cond x y z) = f x <> f y <> f z
hfoldMap f (IsEq x y) = f x <> f yNote that we cannot use the standard class in Data.Foldable as we require the supplied monoid constructor to be polymorphic in the type-index. In fact, to be theoretically correct and avoid problems adding more higher-order analogues, we should really define a type-indexed monoid, but we’ll stop short of that in order to use all the existing monoid instances out there.
Let’s use the above to count the number of expression nodes, making use of hcata and hfoldMap:
size :: Expr a -> Int
size = getSum . unK . hcata alg where
alg :: ExprF (K (Sum Int)) :~> K (Sum Int)
alg x = K $ Sum 1 <> hfoldMap unK xλ> size x
5
λ> size y
8Equality
We are at some point going to want to compare two type-indexed expressions for equality. The simplest way to achieve this would be to created an “untyped” vanilla ADT version of our expression type with a deriving clause for Eq and Ord; and an isomorphism (bijective mapping) between it and our GADT representation. However, with more work, we can arrive at a more efficient and flexible solution.
First we’ll define a new class for defining equality for terms of type f a where a is universally qualified. This is purely a convenience to help arrive ultimately at an instance for Eq (Expr a) without having to create Eq instances for every context and type-index combination.
For our ExprF datatype, we need the following instances:
instance HEq r => Eq (ExprF r a) where
Const x1 == Const x2 = x1 == x2
Add x1 x2 == Add y1 y2 = heq x1 y1 && heq x2 y2
Mul x1 x2 == Mul y1 y2 = heq x1 y1 && heq x2 y2
Cond x1 x2 x3 == Cond y1 y2 y3 = heq x1 y1 && heq x2 y2 && heq x3 y3
IsEq x1 x2 == IsEq y1 y2 = heq x1 y1 && heq x2 y2Let’s test all this equality machinery:
λ> HFix (Const 1) == HFix (Const 1)
True
λ> HFix (Const 1) == HFix (Const 2)
False
λ> x == y
Couldn't match expected type `Bool' with actual type `Int' ...Expressions of the same type index compare with (==), but otherwise we get a type error. This will not always be what we want; a heterogenous equality comparison would allow us to compare expressions with potentially different type indices for equality. One likely use case for this is adding an expression term to a homogeneous container, such as a List, using an existential wrapper:
which we can later eliminate with:
Using the above, a list of our expressions would have type [Some Expr]. To test for membership we would need an additional Eq instance for Some; and the definition would need to make use of a heterogeneous equality test. In order to achieve this, we will unfortunately need to reify the type index into an associated singleton value, so we start by defining these “type tags”:
-- | singleton type tags that witness the expression type at runtime
data Type :: * -> * where
TBool :: Type Bool
TInt :: Type IntThe goal of the above type tags is to deliver evidence to the type-checker that the type indices represented by the tags are equal. For this purpose, we define a new datatype:
We’ll define a new type-class HEqHet to support our heterogeneous equality comparison heqHet; and make use of a helper method heqIdx, which returns evidence of index equality if the indexes are the same type, but ignores the structure. It turns out that this helper method is the only missing piece that we need to implement heterogeneous equality, as heq will take care of structural equality. We can thus provide a default implementation for heqHet which makes use of heqIdx and heq.
class HEq f => HEqHet f where
-- | type-index equality
heqIdx :: f a -> f b -> Maybe (a :=: b)
-- | heterogeneous equality
heqHet :: f a -> f b -> Maybe (a :=: b)
heqHet x y = case heqIdx x y of
Just Refl | x `heq` y -> Just Refl
_ -> NothingFinally, we implement type index equality heqIdx for our type-tag singletons and expression type, needed by the heterogeneous equality heqHet default method.
getType :: Expr a -> Type a
getType e = case unHFix e of
Const {} -> TInt
Add {} -> TInt
Mul {} -> TInt
Cond _ e _ -> getType e
IsEq {} -> TBoolinstance HEqHet Type where
heqIdx TBool TBool = Just Refl
heqIdx TInt TInt = Just Refl
heqIdx _ _ = NothingNow the machinery is in place, let’s try out a heterogeneous equality test:
λ> isJust $ x `heqHet` x
True
λ> isJust $ x `heqHet` y
FalseRecall that the ultimate aim was this:
λ> elem (Some x) [Some x, Some y]
TrueOf course, for tree-based Maps and Sets we will need an Ord instance for Some and Expr. We will omit the classes and instances for Ord in these notes, but the treatment proceeds in a similar fashion as the Eq case.
Example: A tracing evaluator
For a final example that uses many of the constructs we’ve defined so far, we’ll implement a tracing evaluator that returns the values of all the intermediate subterms. To accomplish this, we’ll make use of another recursion scheme, a paramorphism. The supplied function for a paramorphism gets both the recursively computed value and the original subterm used to compute it. A paramorphism is just a convenient way of getting access to the original input structures; it could be defined as a catamorphism, although it would be less efficient to do so.
The definition of a paramorphism can be arrived at by a small modification to our catamorphism, we fmap the lambda \x -> (para alg, x) or alternatively (para alg &&& id), which gives us a the original subterm as the second element of the argument pair.
For vanilla functors, a paramorphism is thus:
para :: Functor f => (f (a, Fix f) -> a) -> Fix f -> a
para psi = psi . fmap (para psi &&& id) . unFixTo define a paramorphism for higher-order functors, we’ll need some additional higher-order analogues:
-- | The higher-order analogue of (&&&) for functor products
(&&&&) :: (f :~> g) -> (f :~> g') -> f :~> (g :*: g')
(&&&&) u v x = u x :*: v x
infixr 3 &&&&-- | Generalised unzip for higher-order functors
hfunzip :: HFunctor h => h (f :*: g) :~> (h f :*: h g)
hfunzip = hfmap hfst &&&& hfmap hsnd-- | paramorphism for higher-order functors
hpara :: HFunctor h => (h (f :*: HFix h) :~> f) -> (HFix h :~> f)
hpara psi = psi . hfmap (hpara psi &&&& id) . unHFixThe tracing evaluator will need to return a container mapping expression subterms to values. We’ll use an association list to avoid needing to define Ord instances:
Note that we have made use of our existential wrapper Some and the value wrapper type Value from earlier. We’ll also demonstrate the use of type-tags and our getType function to recover tagged values for storing into the list.
The implementation of our tracing evaluator is as follows:
evalTrace :: Expr a -> Result
evalTrace = unK . hsnd . hpara psi where
psi :: ExprF ((I :*: K Result) :*: Expr) :~> (I :*: K Result)
psi (hfunzip -> ((hfunzip -> (hv :*: hr)) :*: he)) =
I v :*: (K $ (Some e, v') : m)
where
v = unI . evalAlg $ hv
m = hfoldMap unK $ hr
e = HFix he
v' = mkValue (getType e) vNote that we are of course using an evaluation algebra instead of our eval function introduced earlier, as we do not want to introduce any additional traversals. One disadvantage of using a paramorphism, is that it makes it difficult to arrive at a solution to the above by combining F-algebras.
λ> map (first $ some ppr) $ evalTrace y
[(if (1 + 2) == 3 then 1 else 2,VInt 1),((1 + 2) == 3,VBool True),((1 + 2),VInt 3),(1,VInt 1),(2,VInt 2),(3,VInt 3),(1,VInt 1),(2,VInt 2)]The HFunctor has also proved useful for both nested vanilla algebraic datatypes [1] and generic mutual recursion [2]. Further reading on HFunctor applied to GADTs can be found here [3]. Finally, the literal haskell for this post can be found here.
References
[1] Richard Bird and Lambert Meertens. “Nested Datatypes” (1998): 52–67.
[2] Alexey Rodriguez, Stefan Holdermans, Andres Löh, Johan Jeuring. “Generic programming with fixed points for mutually recursive datatypes” ICFP 2009.
[3] Johann, Patricia, and Neil Ghani. “Foundations for Structured Programming with GADTs.” ACM SIGPLAN Notices 43, no. 1 (January 14, 2008): 297.
In category theory parlance, (Fix f :: , unFix :: f (Fix f) -> Fix f) is the initial algebra* in the category of F-algebras, for which there is a unique homomorphism (the catamorphism) to any other algebra (f a :: *, alg :: f a -> a) in the category.↩︎